The Continuation Value of the American to the Price of the European
Abstract
The critical price \(S^{*}\left( t\right) \) of an American put option is the underlying stock price level that triggers its immediate optimal exercise. We provide a new perspective on the determination of the critical price near the option maturity T when the jump-adjusted dividend yield of the underlying stock is either greater than or weakly smaller than the riskfree rate. Firstly, we prove that \(S^{*}\left( t\right) \) coincides with the critical price of the covered American put (a portfolio that is long in the put as well as in the stock). Secondly, we show that the stock price that represents the indifference point between exercising the covered put and waiting until T is the European-put critical price, at which the European put is worth its intrinsic value. Finally, we prove that the indifference point's behavior at T equals \(S^{*}\left( t\right) \)'s behavior at T when the stock price is either a geometric Brownian motion or a jump-diffusion. Our results provide a thorough economic analysis of \(S^{*}\left( t\right) \) and rigorously show the correspondence of an American option problem to an easier European option problem at maturity .
Introduction
American options are important derivatives with a variety of applications in financial economics including perpetual rights (e.g. Henderson and Hobson (2008)), portfolios of rights (e.g. Henderson et al. (2014)), corporate security valuation (e.g. Black and Cox (1976); Geske (1977), and Vidal Nunes (2011)), and contracts with complex embedded decisions (e.g. Gerer and Dorfleitner (2018), and Battauz et al. (2020)). There is a vast literature on the close-to-maturity valuation of finite-maturity American options (e.g. Barles et al. 1995; Pham 1997; Evans et al. 2002; Lamberton and Villeneuve 2003; Detemple 2005; Lamberton and Mikou 2008; Bouselmi and Lamberton 2016; Li 2010a, b and Cheng and Zhang 2012). A finite-maturity American put option on a stock requires optimal early exercise as soon as the current underlying stock price \(S\left( t\right) \) is not above an endogeneous time-varying barrier called the critical price \(S^{*}\left( t\right) \). If the riskfree rate dominates the jump-adjusted dividend yield of the underlying stock, \(S^{*}\left( t\right) \) converges to the strike price K as t approaches the maturity date T. Remarkably, if the jump-adjusted dividend yield is greater than the riskfree rate, the American-put critical price at maturity displays a discontinuity as \( S^{*}\left( t\right) \) converges to a limit strictly smaller than \(K=S^*(T)\). Given a geometric Brownian motion for the underlying stock price, Ingersoll (1998) offers an intuitive indifference-point argument to economically assess such a discontinuity. Similar arguments can be found in Kim and Yu (1996) and Huang et al. (1996).
We contribute by providing a new perspective on the determination of the critical price at maturity when the jump-adjusted dividend yield is either greater than or weakly smaller than the riskfree rate r. The jump-adjusted dividend yield is the sum of the stock's payout rate q, i.e. the classical dividend yield, and of the stock's expected return due to upward jumps (see Theorem 4.2). In the absence of jumps, the jump-adjusted dividend yield equals q. Our method brings in exactness and validity across two relevant stock price models without giving away financial intuition. We follow Ingersoll (1998) in employing an indifference-point analysis on the optimal exercise of a covered American put, which here is taken to be a portfolio that is long in the put option as well as in one underlying share. However, our novel approach is more rigorous, as it performs a careful study of the early exercise premium, and it applies to a jump-diffusion setting. Additionally, our approach can justify the Ingersoll (1998) argument as one of its implications.
In a Black and Scholes (1973) setting, Ingersoll (1998) claims that \( S^{*}\left( t\right) \) near maturity (at \(t=T-dt\)) coincides with the indifference point where the payoff from the covered put immediate exercise and the present value of the covered put terminal cashflow coincide. In particular, if you exercise the covered American put at \( t=T-dt\) when \(S\left( t\right) =x\) to sell the stock, you get
$$\begin{aligned} \left( K-x\right) ^{+}+x=\left\{ \begin{array}{lll} K &{} &{} \text {if }K>x \\ &{} &{} \\ x &{} &{} \text {if }K\le x \end{array} \right. \end{aligned}$$
On the contrary if you continue until \(T=t+dt\), the value in t of the cashflow you will get in T is approximately
$$\begin{aligned} \underset{ \begin{array}{c} \text {value at }t\text { of }K \\ \text {obtained at }T=t+dt \\ \text {from the exercise of the} \\ \text {covered put} \end{array} }{\underbrace{Ke^{-r\ dt}}}+\underset{ \begin{array}{c} \text {dividends earned at }t \\ \text {for holding the stock from }t\text { to }T=t+dt\text { } \end{array} }{\underbrace{xqdt}} \end{aligned}$$
when x is smaller than K. According to Ingersoll, given \(x<K,\) the critical price \( S^{*}\left( t\right) =x^{*}\) is the indifference point \( x=x^{*}\) such that the two cashflows coincide (please note that \(x^{*}\) is a function of dt), namely \(x^{*}\) is the solution of
$$\begin{aligned} K=Ke^{-r\ dt}+x^{*}qdt \end{aligned}$$
(1.1)
Equation (1.1) compares K, the immediate payoff from the exercise of the in the money covered put at \(t=T-dt,\,\)to the value in t of the cashflow you will get in T provided that the option closes at maturity in the money, \(Ke^{-r\,dt}+xqdt.\) The right hand side term in equation (1.1) is the present value at \(t=T-dt\) of the continuation value of the covered put option, without risk-adjustment.
This equation is financially intuitive but inaccurate: it cannot be related to the standard definition of the value of an American option and of the critical price. The argument suggested by Ingersoll requires that the optimal policies (namely, optimal exercise date and critical price \(S^{*}\left( t\right) \)) for the American covered and uncovered put options coincide at maturity. Such identification is not trivial, because the American put option and the covered American put option have different payouts, since the latter includes a long position in the underlying stock as well as the implied dividend stream.
Firstly, we prove that \(S^{*}\left( t\right) \) coincides with the critical price of the covered American put during the whole life of the options under the mere assumption of Markovian dynamics for the underlying stock price. Secondly, we show that the underlying price that represents the indifference point between exercising the covered put and waiting until maturity is the European-put critical price, at which the European put is worth its intrinsic value. Finally, we prove that its behavior at maturity is the same as the American-put critical price when the underlying stock price follows either a lognormal diffusive dynamics or a jump-diffusive dynamics.
Our findings economically and technically add to the rich literature on the close-to-maturity patterns of the critical price. We are the first to validate the computational equivalence of an American option problem to an easier European one at maturity under the geometric Brownian motion and jump-diffusion models. Since the non-inclusion of the early exercise premium makes calculations much easier, our results are auspicious for the investigation of the possibly discontinuous American-put critical price at maturity under more complicated models.
The paper is organized as follows. In Section 2, we prove that the optimal exercise policies of the covered and uncovered puts are identical. In Section 3, we show that indifference-point argument characterizes the critical price of the European put, whose existence and uniqueness are also proved. In Section 4, we analyze the behavior of the European-put critical price both in a geometric Brownian motion model and in a jump-diffusion model, showing that it mimics at maturity the behavior of the critical price of an American put option. Section 5 concludes.
The critical price of the covered put
Let \((S\left( t\right) )_{0\le t\le T}\) be the price of a financial asset in an arbitrage-free market modeled as a a filtered probability space \( \left( \Omega ,\left( {\mathcal {F}}_{t}\right) _{0\le t\le T},{\mathcal {F}}, {\mathbb {P}}\right) \), where we assume that \({\mathbb {P}}\) is the risk-neutral probability and \(\left( {\mathcal {F}}_{t}\right) _{0\le t\le T}\) is the filtration generated by \((S\left( t\right) )_{0\le t\le T}\), properly completed as to satisfy the usual assumptions. The risk-neutral dynamics of \( S\left( t\right) \) is given by
$$\begin{aligned} S\left( t\right) =S_{0}e^{(r-q)t+L_{t}} \end{aligned}$$
where r is the riskless interest rate, q the dividend yield and \(L_{t}\) a real Lévy process, such that the process \(e^{-(r-q)t}S\left( t\right) \) is a martingale. For sake of simplicity, we denote by \({{\mathbb {E}}_{t}}\) the conditional expectation with respect to \({\mathcal {F}}_{t}\).
The value of an American put option written on the asset S, with strike price K and maturity T is
$$\begin{aligned} V\left( t\right)= & {} \mathrm {ess}\sup _{t\le \tau \le T}{{{\mathbb {E}}_t}} \left[ e^{{-}r\left( \tau -t\right) }\left( K-S(\tau )\right) ^{+}\right] \nonumber \\= & {} {{{\mathbb {E}}_t}}\left[ e^{{-}r\left( \tau ^{*}-t\right) }\left( K-S(\tau ^{*})\right) ^{+}\right] =v(t,S(t)) \end{aligned}$$
(2.1)
where \(\tau ^*\) is the optimal exercise policy,
$$\begin{aligned} v(t,x)=\sup _{0\le \Theta \le T-t}{{{\mathbb {E}}}}\left[ e^{{-}r\Theta }\left( K-x\cdot e^{ \left( r-q \right) \Theta +L(\Theta )} \right) ^{+}\right] \end{aligned}$$
and the last equality in (2.1) is due to the Markov property of Lévy processes. When Footnote 1 \(r\ge 0,\) it is well known that the free boundary consists of the graph of the critical price
$$\begin{aligned} S^{*}(t)=\sup \left\{ x\ge 0:v(t,x)=K-x\right\} \le K, \end{aligned}$$
(2.2)
and the option is optimally exercised at t if \(S(t)\le S^{*}(t).\)
A covered put option is the strategy of holding the underlying stock S and the American put on S. Thus the optimal exercise policy \( \tau _{c}^{*}\) is the one the maximizes the expected gain due to the immediate payoff gained at \(\tau _{c}^{*}\), namely \(\left( K-S(\tau _{c}^{*})\right) ^{+}+S(\tau _{c}^{*}) \) and to the dividend stream gained until \(\tau _{c}^{*}.\) The dividends payed between s and \(s+ds\) are \(S(s)qds.\, \ \)Investing the dividends instantaneosly at the risk free rate r we get at \(\tau _{c}^{*}\) the (capitalized) dividend stream
$$\begin{aligned} \int \limits _{0}^{\tau _{c}^{*}}S(s)e^{r\left( \tau _{c}^{*}-s\right) }qds. \end{aligned}$$
Thus the value of the covered option \(V^{c}\) is given by
$$\begin{aligned} V^{c}\left( t\right) =\mathrm {ess}\sup _{t\le \tau \le T}{{{\mathbb {E}}_t}} \left[ e^{{-}r\left( \tau -t\right) }\left( \left( K-S(\tau )\right) ^{+}+S(\tau )+\int \limits _{0}^{\tau }S(s)e^{r\left( \tau -s\right) }qds\right) \right] \end{aligned}$$
(2.3)
and \(\tau _{c}^{*}\) is the stopping time that reaches the sup in (2.3). It is not obvious that \(\tau _{c}^{*}\) coincides with the optimal stopping time for the American option \(\tau ^{*}\) in (2.1): our next aim is to prove that indeed the two optimal exercise policies coincide. Let G be the gain process from holding 1 unit of S. In discounted terms \({\widetilde{G}}\) is
$$\begin{aligned} {\widetilde{G}}\left( t\right) ={\widetilde{S}}(t)+\int \limits _{0}^{t} {\widetilde{S}}(s)qds \end{aligned}$$
Note that \({\widetilde{G}}\) is a martingale, since
$$\begin{aligned} {\widetilde{G}}\left( t\right) = {\widetilde{G}}\left( 0\right) + \int _0^t e^{-qs} d \left( e^{qs} {\widetilde{S}}(s)\right) = {\widetilde{G}}\left( 0\right) + \int _0^t e^{-qs} d \left( e^{-(r-q)s} {S}(s)\right) . \end{aligned}$$
In the next proposition, we prove that the value of the American covered put is given by the sum of the value of the American put and the gain of holding the underlying asset and, as a consequence, the optimal exercise policies of the American covered and uncovered put options coincide.
Proposition 2.1
When \(q\ge 0,\) we have that \(V+G=V^{c} \) and \( \tau _{c}^{*}=\tau ^{*}. \)
Proof
Denote with \(\widetilde{\left( \cdot \right) }\) the discounted values, e.g. \({\widetilde{V}}\left( t\right) =V\left( t\right) e^{-rt}.\) It is well known that \({\widetilde{V}}\) as in (2.1) is the smallest supermartingale dominating the immediate discounted put payoff \({\widetilde{X}}\left( t\right) =\left( K-S\left( t\right) \right) ^{+}e^{-rt}\ge 0\) (Theorem 2.15 in El Karoui 1981). When \(q\ge 0,\) the discounted payoff of the covered put is always non negative
$$\begin{aligned} \widetilde{X^{c}}\left( t\right) ={\widetilde{X}}(t)+{\widetilde{S}}(t)+\int \limits _{0}^{t}{\widetilde{S}}(s)qds\ge 0. \end{aligned}$$
Therefore Theorem 2.15 in El Karoui (1981) also ensures that \(\widetilde{V^{c} }\) in (2.3) is the smallest supermartingale dominating \( \widetilde{X^{c}}.\) We use these two properties to prove our theorem. The process \(\widetilde{V^{c}}-{\widetilde{G}}\) is a supermartingale as well, since \({\widetilde{G}}\) is a martingale. Moreover \(\widetilde{V^{c}}-{\widetilde{G}}\) dominates \({\widetilde{X}},\) because
$$\begin{aligned} \widetilde{V^{c}}\left( t\right) -{\widetilde{G}}\left( t\right)&\ge \widetilde{X^{c}}\left( t\right) -{\widetilde{G}}\left( t\right) =\left( {\widetilde{X}}\left( t\right) +{\widetilde{S}}\left( t\right) +\int \limits _{0}^{t}{\widetilde{S}}(s)qds\right) -{\widetilde{G}}\left( t\right) = {\widetilde{X}}\left( t\right) \text {.} \end{aligned}$$
Since \({\widetilde{V}}\) is the smallest supermartingale dominating \({\widetilde{X}}\), we have \({\widetilde{V}}\left( t\right) \le \widetilde{V^{c}}\left( t\right) -{\widetilde{G}}\left( t\right) \) for all t, hence
$$\begin{aligned} {\widetilde{V}}(t) +{\widetilde{G}}(t) \le \widetilde{V^{c}}(t) \qquad \text{ for } \text{ all } t . \end{aligned}$$
We have now to prove the opposite inequality. To this aim, note that the process \({\widetilde{V}}+{\widetilde{G}} \) is the sum of the supermartingale \( {\widetilde{V}}\) and the martingale \({\widetilde{G}}\) and therefore a supermartingale as well. Moreover
$$\begin{aligned} {\widetilde{V}}\left( t\right) +{\widetilde{G}}\left( t\right) \ge {\widetilde{X}} \left( t\right) +{\widetilde{S}}(t)+\int \limits _{0}^{t}{\widetilde{S}}(s)qds= \widetilde{X^{c}}\left( t\right) . \end{aligned}$$
Therefore
$$\begin{aligned} {\widetilde{V}}\left( t\right) +{\widetilde{G}}\left( t\right) \ge \widetilde{ V^{c}}\left( t\right) \qquad \text{ for } \text{ all } t \end{aligned}$$
because \(\widetilde{V^{c}}\) is the smallest supermartingale dominating \( \widetilde{X^{c}}.\) This proves that \({\widetilde{V}}\left( t\right) + {\widetilde{G}}\left( t\right) =\widetilde{V^{c}}\left( t\right) .\) This equality implies that
$$\begin{aligned} \tau _{c}^{*}&=\inf \left\{ t:V^{c}\left( t\right) =X^{c}\left( t\right) \right\} \\&=\inf \left\{ t:V\left( t\right) +G\left( t\right) =X^{c}\left( t\right) \right\} \\&=\inf \left\{ t:V\left( t\right) +G\left( t\right) =X(t)+G\left( t\right) \right\} \\&=\inf \left\{ t:V\left( t\right) =X(t)\right\} =\tau ^{*}. \ \end{aligned}$$
\(\square \)
Remark 2.1
The previous proposition holds under no-arbitrage independently on the dynamics of the underlyingS.
In the next proposition we exploit the Markov property of the Lévy process to show that the value of the American covered put is a deterministic function of t, and current levels of G and S. We also prove that it is additive with respect to the current dividend stream, property which turns out fundamental in proving that the critical prices of the covered and uncovered put coincide.
Proposition 2.2
The discounted value of the covered put is
$$\begin{aligned} {\widetilde{V}}^{c}\left( t\right)&=\mathrm {ess}\sup _{t\le \tau \le T}{{ {\mathbb {E}}_t}}\left[ e^{{-}r\tau }\left( K-S(\tau )\right) ^{+}+{\widetilde{G}} (\tau ) \right] \\&={{{\mathbb {E}}}_t}\left[ e^{{-}r\tau _{c}^{*}}\left( K-S(\tau _{c}^{*})\right) ^{+}+{\widetilde{G}}(\tau _{c}^{*}) \right] ={\widetilde{v}}^{c}(t,S(t),G\left( t\right) ) \end{aligned}$$
where
$$\begin{aligned} {\widetilde{v}}^{c}(t,x,g)=e^{-rt}\sup _{0\le \Theta \le T-t} {{{\mathbb {E}}}} \left[ e^{-r\Theta } \left( K-x\cdot e^{(r-q) \Theta + L(\Theta ) } \right) ^{+} + g + x f\left( \Theta \right) \right] \end{aligned}$$
(2.4)
with
$$\begin{aligned} f\left( \Theta \right) = e^{ -q \Theta +L(\Theta )}-1 +\int \limits _{0}^{\Theta }e^{ -q s+ L(s)}qds. \end{aligned}$$
In addition, for all \(t\in \left( 0,T\right) ,\) \({\widetilde{g}}=ge^{-rt}\) and \({\widetilde{x}}=xe^{-rt},\) we have that
$$\begin{aligned} {\widetilde{v}}^{c}(t,x,g)={\widetilde{v}}^{c}(t,x,0)+{\widetilde{g}}, \end{aligned}$$
(2.5)
Proof
We can write
$$\begin{aligned} {\widetilde{G}}\left( \tau \right) ={\widetilde{G}}\left( t\right) +{\widetilde{S}} (\tau )-{\widetilde{S}}(t)+\int \limits _{t}^{\tau }{\widetilde{S}}(s)qds \end{aligned}$$
Letting \(\Theta =\tau -t,\) \({\widetilde{G}}\left( t\right) =\widetilde{g} =ge^{-rt}\) and \({\widetilde{S}}(t)={\widetilde{x}}=xe^{-rt},\) we have
$$\begin{aligned} {\widetilde{G}}\left( \tau \right) ={\widetilde{g}}+{\widetilde{x}}\left( e^{-q \left( \tau -t\right) + L\left( \tau \right) -L\left( t\right) }-1\right) + {\widetilde{x}}\int \limits _{t}^{\tau }e^{ -q \left( s-t\right) + L\left( s\right) -L\left( t\right) }qds, \end{aligned}$$
and thanks to the independence and stationarity properties of the increments of a Lévy process, we can write
$$\begin{aligned} \left. {\widetilde{G}}(\tau )\right| _{{\mathcal {F}}_{t}}&\sim {\widetilde{g}}+{\widetilde{x}}\left( e^{ -q \left( \tau -t\right) +L\left( \tau -t\right) }-1\right) +{\widetilde{x}}\int \limits _{t}^{\tau }e^{ -q \left( s-t\right) +L\left( s-t\right) }qds \\&={\widetilde{g}}+{\widetilde{x}}\left( e^{ -q \Theta +L(\Theta )}-1\right) + {\widetilde{x}}\int \limits _{0}^{\Theta }e^{ -q \theta +L(\theta )}qd\theta \\&= {{\widetilde{g}}} + {{\widetilde{x}}} f\left( \Theta \right) =e^{-rt}\left( g+ x f\left( \Theta \right) \right) \end{aligned}$$
by changing the variable of integration \(\theta =s-t.\) Additivity follows immediately from (2.4). \(\square \)
The critical price at t of the covered put option is
$$\begin{aligned} S_{c}^{*}(t,g)=\sup \left\{ x\ge 0:{\widetilde{v}}^{c}(t,x,g)=\left( e^{{-} rt}K-{\widetilde{x}}\right) ^{+}+{\widetilde{g}}\right\} \end{aligned}$$
From the above definition, which is the analogous of definition (2.2) for the (uncovered) put option, we see that \(S_{c}^{*} \) depends on both t and g. On the other hand, the additivity of the discounted value of the American put option with respect to g, implies that \(S_{c}^{*}\) is independent of g, because
$$\begin{aligned} S_{c}^{*}(t,g)&=\sup \left\{ x\ge 0:{\widetilde{v}}^{c}(t,x,g)=\left( e^{ {-}rt}K-{\widetilde{x}}\right) ^{+}+{\widetilde{g}}\right\} \\&=\sup \left\{ x\ge 0:{\widetilde{v}}^{c}(t,x,0)+{\widetilde{g}}=\left( e^{{-} rt}K-{\widetilde{x}}\right) ^{+}+{\widetilde{g}}\right\} \\&=\sup \left\{ x\ge 0:{\widetilde{v}}^{c}(t,x,0)=\left( e^{{-}rt}K- {\widetilde{x}}\right) ^{+}\right\} \\&=S_{c}^{*}(t,0)=S_{c}^{*}(t). \end{aligned}$$
This will allows us to identify the critical prices of the covered and uncovered American put options.
Theorem 2.3
(Critical prices of covered and uncovered put coincide). For all \(t\in \left( 0,T\right) \) we have that \( S_{c}^{*}(t)=S^{*}(t).\)
Proof
From Proposition 2.1 we have that \(V+G=V^{c}\), which implies
$$\begin{aligned} {\widetilde{v}}(t,S(t))+{\widetilde{G}}\left( t\right) ={\widetilde{v}} ^{c}(t,S(t),G\left( t\right) )\text { for all }t,S(t),G(t) \end{aligned}$$
namely \({\widetilde{v}}(t,x)+{\widetilde{g}}={\widetilde{v}}^{c}(t,x,g)\) for all t,x,g. Equation (2.5) implies
$$\begin{aligned} {\widetilde{v}}(t,x)+{\widetilde{g}}={\widetilde{v}}^{c}(t,x,0)+{\widetilde{g}}\text { for all }t,x,g \end{aligned}$$
leading to
$$\begin{aligned} {\widetilde{v}}(t,x)={\widetilde{v}}^{c}(t,x,0)\text { for all }t,x \end{aligned}$$
And therefore
$$\begin{aligned} S_{c}^{*}(t)&=S_{c}^{*}(t,0)=\sup \left\{ x\ge 0:{\widetilde{v}} ^{c}(t,x,0)=\left( e^{{-}rt}K-{\widetilde{x}}\right) ^{+}\right\} \\&=\sup \left\{ x\ge 0:{\widetilde{v}}(t,x)=\left( e^{{-}rt}K-{\widetilde{x}} \right) ^{+}\right\} \\&=\sup \left\{ x\ge 0:v(t,x)=\left( K-x\right) ^{+}\right\} =S^{*}(t).\ \end{aligned}$$
\(\square \)
The critical price of the European put option
In this section, we try to apply rigorously Ingersoll's argument in order to find the critical price of the covered put option. The idea is to compare K, the immediate payoff from the exercise of the in/at the money covered put at \(t=T-dt,\,\)to the value in t of the cashflow you will get in T provided that the option closes at maturity in the money, \(Ke^{-r\ dt}+xqdt\) (see Eq. (1.1)). Formally, if one waits till maturity to exercise the option, the present value at time \(T-dt\) is the value of the corresponding covered European put option plus the present value of the gain from dividends, that is
$$\begin{aligned} e^{-rdt}{{{\mathbb {E}}}}_{T-dt}\left[ \left( K-S\left( T\right) \right) ^{+}+S\left( T\right) + \int _{T-dt}^T e^{r(T-s)} S\left( s\right) qds\right] . \end{aligned}$$
(3.1)
We consider the indifference point \(S(T-dt) = x\) that renders expression (3.1) equal to K. The following proposition shows that such an indifference point is also the critical price of the European put option, defined as the underlying stock price level \(x^*\) such that the European put value coincides with the intrinsic value.
Proposition 3.1
Let \(\varepsilon > 0\) be the time to maturity. The indifference point \(x(\varepsilon )=S(T-\varepsilon )\) which solves equation
$$\begin{aligned} K=e^{-r\varepsilon } {{\mathbb {E}}}_{T-\varepsilon }\left[ \left( K-S\left( T\right) \right) ^{+}+S\left( T\right) + \int _{T-\varepsilon }^T e^{r(T-s)} S\left( s\right) qds\right] \end{aligned}$$
(3.2)
is the solution of
$$\begin{aligned} K-x = p\left( x , \varepsilon \right) \end{aligned}$$
(3.3)
where \(p(x,\varepsilon )\) denotes the price at \(T-\varepsilon \) of an European put option on S with maturity T and strike price K, when \( S(T-\varepsilon )=x\).
Proof
Equation (3.2) can be written as
$$\begin{aligned} K= p\left( x , \varepsilon \right) + e^{-r\varepsilon } {{\mathbb {E}}} _{T-\varepsilon }\left[ S\left( T\right) + \int _{T-\varepsilon }^T e^{r(T-s)} S\left( s\right) qds\right] . \end{aligned}$$
Since
$$\begin{aligned} e^{-r\varepsilon } \, {\mathbb {E}}_{T-\varepsilon } \left[ S(T) + \int _{T-\varepsilon }^T e^{r(T - s)} S(s) q ds \right]= & {} {\mathbb {E}} _{T-\varepsilon } \left[ e^{-r\varepsilon } S(T)\right] \\&+ \int _{T-\varepsilon }^T {\mathbb {E}}_{T-\varepsilon } \left[ e^{-r(s-(T- \varepsilon ))} S(s)\right] q ds \\= & {} e^{-q\varepsilon } S(T-\varepsilon ) \\&+ S(T-\varepsilon )\,\int _{T-\varepsilon }^T e^{-q(s-(T-\varepsilon ))} q ds \\= & {} e^{-q\varepsilon } x +x \left( 1-e^{-q\varepsilon } \right) = x \end{aligned}$$
the claim follows. \(\square \)
At a first glance, Eq. (3.3) seems different from Ingersoll's Eq. (1.1). However, exploiting the put-call parity, we have that \(p\left( x , \varepsilon \right) = c\left( x , \varepsilon \right) - x e^{-q\varepsilon } + K e^{-r\varepsilon }\) where \( c(x,\varepsilon )\) denotes the price at \(T-\varepsilon \) of an European call option on S with maturity T and strike price K, when \( S(T-\varepsilon )=x\). Simple algebra shows then that Equation (3.3) is equivalent to
$$\begin{aligned} K = Ke^{-r\varepsilon } + xq\varepsilon +c(x,\varepsilon ) + x {\mathcal {R}} (\varepsilon ) \end{aligned}$$
(3.4)
with \({\mathcal {R}}(\varepsilon ) = 1 - e^{-q\varepsilon } - q\varepsilon \). This equation resembles Ingersoll's equation: it differs from it only for the last two terms in the right-hand side which both go to 0 as maturiy approaches, if the put option is in the money (hence the call option is out of the money). More precisely, the term \({\mathcal {R}}(\varepsilon ) \) goes to 0 faster than \(\varepsilon \). In the next section we will analyze the behavior of the term \(c(x,\varepsilon )\) close to maturity in two cases where the price of the call option is given in closed form: when the price of the asset has a lognormal dynamics and when it evolves according to a jump-diffusion process.
The following lemma shows that Eq. (3.3), or equivalently (3.4) admits a unique solution Footnote 2 for every \(\varepsilon >0\).
Lemma 3.1
For every \(\varepsilon >0\), Eq. (3.3) admits a unique solution \(x=x(\varepsilon ) \in (0,K]\).
Proof
Define \(\varphi (x) =p(x,\varepsilon )+x\). The function \(\varphi \) is continuous, differentiable and strictly increasing on (0,K], since \(\varphi ^{\prime }(x)=1 +p_{x}(x,\varepsilon )>0\) where \(p_{x}= \frac{\partial p}{\partial x}\) is the delta of the put option, which is always greater than -1. Moreover \(\lim _{x\rightarrow 0^{+}}\varphi (x)<K \le \varphi (K)\). Indeed \(\lim _{x\rightarrow 0^{+}}\varphi (x)=\lim _{x \rightarrow 0^{+}} p(x, \varepsilon ) = Ke^{-r\varepsilon } < K\). On the other hand \(\varphi (K) = p(K, \varepsilon ) + K \ge K\). Hence necessarily Eq. (3.3) admits a unique solution. \(\square \)
We have just shown that the indifference price identified by Ingersoll is essentially the critical price of the European option, whose existence is proved in the above lemma. We want now to show that close to maturity this point is a good approximation for the critical price of the American option. It is well known that the last is the highest value for which the continuation value of the option is equal to the immediate payoff. In fact equation
$$\begin{aligned} K-y = v(T-\varepsilon , y) \end{aligned}$$
(3.5)
admits an interval of solutions \((0, y(\varepsilon )] \in (0,K]\), where \( y(\varepsilon )\) is the critical price. The right hand side of Eq. (3.5) can be written as \(p(y,\varepsilon ) + \Delta (y, \varepsilon )\) where \(\Delta (y, \varepsilon ) = v(T-\varepsilon , y) - p(y, \varepsilon )\) is the early exercise premium. Since \(\Delta (y, \varepsilon ) \ge 0\), we see that \(y(\varepsilon ) \le x(\varepsilon )\le K\) for all \( \varepsilon \). Moreover, Lamberton and Mikou (2008) proved that that \( y(\varepsilon )\) admits a limit \(y^*\in (0, K]\) when \(\varepsilon \) goes to 0, since it is an nondecreasing function of current time. Assuming that \( x(\varepsilon )\) admits a limit as \(\varepsilon \rightarrow 0\), we can see that it converges to the same limit as \(y(\varepsilon )\).
Indeed, equations \(K-x(\varepsilon )=p(x(\varepsilon ), \varepsilon )\) and \( K-y(\varepsilon )=p(y(\varepsilon ), \varepsilon ) + \Delta (y(\varepsilon ), \varepsilon )\) imply that
$$\begin{aligned}&x(\varepsilon )-y(\varepsilon ) = p(y(\varepsilon ), \varepsilon ) - p(x(\varepsilon ), \varepsilon )+ \Delta (y(\varepsilon ), \varepsilon ) \\&\quad = - p_x(x(\varepsilon ), \varepsilon ) \left[ x(\varepsilon )-y(\varepsilon ) \right] - p_{xx}(z(\varepsilon ), \varepsilon ) \frac{ \left( x(\varepsilon )-y( \varepsilon ) \right) ^2}{2}+ \Delta (y(\varepsilon ), \varepsilon ) \end{aligned}$$
where \(y(\varepsilon ) \le z(\varepsilon ) \le x(\varepsilon )\). Hence
$$\begin{aligned} \left[ 1+ p_x(x(\varepsilon ), \varepsilon ) + p_{xx}(z(\varepsilon ), \varepsilon ) \frac{ \left( x(\varepsilon )-y(\varepsilon ) \right) }{2}\right] \left[ x(\varepsilon )-y(\varepsilon ) \right] =\Delta (y(\varepsilon ), \varepsilon ) \end{aligned}$$
Since the early exercise premium \(\Delta (y(\varepsilon ), \varepsilon ) \) tends to 0 as \(\varepsilon \rightarrow 0\), and, in addition, \(1+ p_x(x(\varepsilon ), \varepsilon ) \ge 0\) and \(p_{xx}(z(\varepsilon ), \varepsilon ) > 0\) then \( [x(\varepsilon )-y(\varepsilon )]\) must tend to 0 as well.
Figure 1 shows the behavior of the American (black dots) and European (grey circles) critical prices when the underlying follows a geometrical Brownian motion, for both cases \(r \ge q\) and \(r< q\). The American critical price has been computed via binomial approximation with 125 time steps. The grey diamonds represent the upper and the lower branches of the binomial tree starting at \(t=0\) at \(S(0)=K=1.\) The European critical price has been obtained numerically solving Eq. (3.3). Near maturity T the American and European critical prices are indistinguishable in both cases \(r \ge q\) and \(r< q\). In the latter case, the European and the American critical prices notably converge at maturity to \(K\frac{r}{q}<K\).
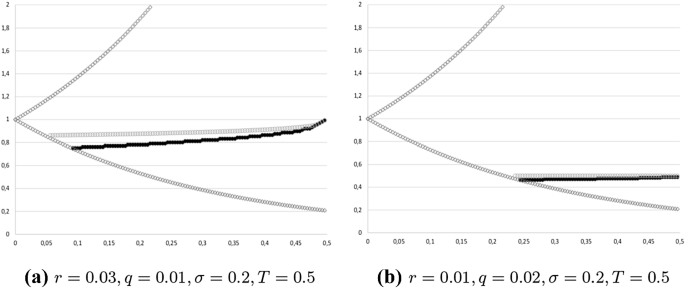
American (black) vs European (grey) critical price (the stock price is a geometric Brownian motion)
In the next section we provide a simple derivation of \(\lim _{\varepsilon \rightarrow 0} x(\varepsilon )\), which allows us to retrieve the well-known results for the limit of the critical price of the American option in the Black-Scholes and the jump-diffusion models. Our considerations may lead to use this approach in more general models.
Critical price at maturity
In this section, we analyze the indifference point of Ingersoll's equation, \( x(\varepsilon )\) close to maturity, both in the Black-Scholes model and in the more general jump-diffusion model.
In what follows, we assume Footnote 3 that \(\lim _{\varepsilon \rightarrow 0^{+}}x(\varepsilon )\) exists. Being \(x(\varepsilon )\in (0,K]\) this limit will be either K or \(x^{*}<K\). Theorems 4.1 and 4.2 will show that the limit coincide with the critical price at maturity of the corresponding American option.
The diffusive case
Assume that \(L_t = \sigma W_t - \frac{\sigma ^2}{2} t\), where \( \left( W_t\right) _{0\le t \le T}\) is a standard brownian motion. In other words, we consider the Black-Scholes model with continuous-dividend payments. The next lemma shows the different behavior of the European call option depending on whether the option at maturity remains out of the money or reaches the at the money-level. The proof is rather technical and can be found in the appendix.
Lemma 4.1
Let \(x(\varepsilon )\) be the solution of Equation (3.3), or equivalently, (3.4). The function \(x(\varepsilon )\) is continuous and differentiable on (0,T). Moreover:
- (i)
If \(\lim _{\varepsilon \rightarrow 0^+} x(\varepsilon )=K\), then \( \lim _{\varepsilon \rightarrow 0^+}\frac{c(x(\varepsilon ),\varepsilon )}{ \varepsilon }=K\left( r-q\right) .\)
- (ii)
If \(\lim _{\varepsilon \rightarrow 0^+}x(\varepsilon )=x^{*}<K\) , then \(\lim _{\varepsilon \rightarrow 0^+}\frac{c(x(\varepsilon ),\varepsilon ) }{\varepsilon }=0.\)
We are now ready to characterize the behavior at maturity of \( x(\varepsilon ) \), when \(r \ge q\) and when \(r < q\). Note in particular, that in the last case, since \(\lim _{\varepsilon \rightarrow 0}\frac{ c(x(\varepsilon ),\varepsilon )}{\varepsilon } = 0\), we recover Ingersoll's equation.
Theorem 4.1
- 1.
If \(0\le q\le r\) then \(\lim _{\varepsilon \rightarrow 0^+} x(\varepsilon )= K\).
- 2.
If \(q>r\) then then \(\lim _{\varepsilon \rightarrow 0^+} x(\varepsilon )= x^* =K \frac{r\ }{q}<K\)
Proof
- 1.
From Equation (3.4), we obtain
$$\begin{aligned} x(\varepsilon )\left( q + \frac{{\mathcal {R}}(\varepsilon )}{\varepsilon }\right) = \frac{K-Ke^{-r\varepsilon }}{\varepsilon }-\frac{c(x(\varepsilon ),\varepsilon ) }{\varepsilon } \end{aligned}$$
(4.1)
Passing to the limit \(\varepsilon \rightarrow 0\), and denoting \( x^*=\lim _{\varepsilon \rightarrow 0^+} x(\varepsilon )\), we have
$$\begin{aligned} x^{*}q=rK-\lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{\varepsilon } \end{aligned}$$
We know that \(x^{*}\le K.\) Assume by contradiction that \(x^{*}<K\). Then the previous lemma implies that \(\lim _{\varepsilon \rightarrow 0}\frac{ c(x(\varepsilon ),\varepsilon )}{\varepsilon }=0\), and therefore \(x^{*}q=rK\) , leading to
$$\begin{aligned} x^{*}=K\frac{r}{q}\ge K, \end{aligned}$$
which is a contradiction. Hence \(x^{*}=K.\)
- 2.
Suppose by contradiction that \(\lim _{\varepsilon \rightarrow 0}x(\varepsilon )=x^{*}=K\). Our previous lemma yields \( \lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{ \varepsilon }=K\left( r-q\right) <0,\) which is an absurd (because the limit of the positive function \(\frac{c(x(\varepsilon ),\varepsilon )}{\varepsilon } \ge 0 \) cannot be negative).
\(\square \)
The jump diffusion case
Assume now that
$$\begin{aligned} L(t) = \left( -\frac{\sigma ^2}{2} - m\lambda \right) t + \sigma W(t) + \sum _{j=1}^{N(t)} U_j \end{aligned}$$
where \((W(t))_{0\le t \le T}\) is a standard brownian motion, N is a Poisson process with intensity \(\lambda \) and \(U_j\) are i.i.d random variables with distribution \(\mu \) such that \({\mathbb {E}}\left[ e^{U_j}\right] = \int e^u \mu (du) = 1+m\). Equation (3.4) is still valid but in this case, the price of the call options is given by
$$\begin{aligned} c(x, \varepsilon ) = \sum _{n = 0}^{+\infty } e^{-\lambda \varepsilon } \frac{ (\lambda \varepsilon )^n}{n!} c_n(x, \varepsilon ) \end{aligned}$$
where \(c_n(x, \varepsilon ) = {\mathbb {E}}_{T- \varepsilon } \left[ e^{-r \varepsilon } (S(T)-K)^+ | S({T- \varepsilon }) = x, N(T) - N({T- \varepsilon } ) = n\right] \) denote the price at time \(T-\varepsilon \) of a European call option on S with maturity T, strike price K, when there are exactly n jumps in the time interval \([T-\varepsilon , T]\). In analogy with the diffusive case, we analyze the behavior of the price of the call option when maturity approaches. The proof of the lemma can be found in the Appendix.
Lemma 4.2
Let \(x(\varepsilon )\) be the solution of Equation (3.3), or equivalently, (3.4). The function \(x(\varepsilon )\) is continuous and differentiable on (0,T). Moreover:
- (i)
\(\displaystyle \lim _{\varepsilon \rightarrow 0} \, \frac{1}{\varepsilon } \sum _{n \ge 2 } e^{-\lambda \varepsilon } \frac{{(\lambda \varepsilon )}^n}{n!} c_n(x(\varepsilon ), \varepsilon ) =0\).
- (ii)
If \(\lim _{\varepsilon \rightarrow 0^+}x(\varepsilon )=x^{*} \le K\), then \(\displaystyle \lim _{\varepsilon \rightarrow 0} \lambda c_1(x(\varepsilon ), \varepsilon ) = \int (x^{*} e^y - K)^+ \nu (dy) \) where \(\nu (dy) = \lambda \,\mu (dy)\).
- (iii)
If \(\lim _{\varepsilon \rightarrow 0^+}x(\varepsilon )=x^{*}<K\) , then \(\displaystyle \lim _{\varepsilon \rightarrow 0} \frac{ c_0(x(\varepsilon ), \varepsilon )}{\varepsilon } =0\). Otherwise, if \(\lim _{\varepsilon \rightarrow 0^+}x(\varepsilon )=K\), then \( \displaystyle \lim _{\varepsilon \rightarrow 0} \frac{ c_0(x(\varepsilon ), \varepsilon )}{\varepsilon }\) \( = K\left( r-q - \int ( e^y - K)^+ \nu (dy)\right) \)
In this case the price of the out of the money call is not negligible because jumps may cause the call to be in the money at some time between \(T-\varepsilon \) and T. In particular, being the time interval very short, the probability of having more than one jump is really small, but one can have a jump exactly at maturity so that intituively we have \( S\left( T-\right) =x\) and \(S\left( T\right) \sim xe^{U_{1}}\). Hence
$$\begin{aligned} \lambda e^{-\lambda \varepsilon }c_{1}(x(\varepsilon ),\varepsilon )\sim \lambda E\left[ (x^{*}e^{U_{1}}-K)^{+}\right]= & {} \lambda \int (x^{*}e^{y}-K)^{+}\mu (dy)\\= & {} \int (x^{*}e^{y}-K)^{+}\nu (dy)\qquad \text{ as } \varepsilon \rightarrow 0. \end{aligned}$$
Given these considerations, we can show that also in the jump-diffusion case, the behavior at maturity of the critical price of the European put option mimics the behavior of the critical price of the corresponding American put option. Footnote 4 Importantly, the limiting behavior of \(x(\varepsilon )\) depends on the sign of the constant d, defined below as the difference between the riskfree rate and the jump-adjusted dividend yield, that is the classical dividend yield q augmented with \(\int (e^y-1)^+ \nu (dy)\), namely the stock's expected return due to upward jumps.
Theorem 4.2
Let \(r \ge 0\) and \(d=r-q - \int (e^y-1)^+ \nu (dy)\). Then
- 1.
if \(d \ge 0\) then \(\lim _{\varepsilon \rightarrow 0} x(\varepsilon ) = K \).
- 2.
if \(d < 0 \) then \(\lim _{\varepsilon \rightarrow 0} x(\varepsilon )=x^*<K\), where \(x^*\) is the unique solution of the equation
$$\begin{aligned} Kr=x^*q + \int (x^* e^y - K)^+ \nu (dy). \end{aligned}$$
Proof
- 1.
As in the proof of Theorem 4.1 we take the limit as \(\varepsilon \rightarrow 0\) in Eq. (4.1) and denoting \(x^{*}=\lim _{\varepsilon \rightarrow 0}x(\varepsilon )\) we have
$$\begin{aligned} x^{*}q=rK-\lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{\varepsilon } \end{aligned}$$
where, by Lemma 4.2 (i) and (ii),
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{ \varepsilon }=\lim _{\varepsilon \rightarrow 0}\frac{c_{0}(x(\varepsilon ),\varepsilon )}{\varepsilon }+\int (x^{*}e^{y}-K)^{+}\nu (dy). \end{aligned}$$
Let \(d\ge 0\) and assume by contradiction that \(x^{*}<K\). Then \( \lim _{\varepsilon \rightarrow 0}\frac{c_{0}(x_{\varepsilon },\varepsilon )}{ \varepsilon }=0\) and \(Kr=x^{*}q+\int (x^{*}e^{y}-K)^{+}\nu (dy)\). So, we have
$$\begin{aligned} 0\le & {} Kd=Kr-Kq-K\int (e^{y}-1)^{+}\nu (dy) \\= & {} -(K-x^{*})q-K\left[ \int (e^{y}-1)^{+}\nu (dy)-\int \left( \frac{ x^{*}}{K}e^{y}-1\right) ^{+}\nu (dy)\right] <0 \end{aligned}$$
which yields a contradiction.
- 2.
Given \(d<0\ \), suppose by contradiction that \(x^*=K.\) Then
$$\begin{aligned} 0 \le \lim _{\varepsilon \rightarrow 0} \frac{c_0(x_\varepsilon , \varepsilon )}{ \varepsilon } = Kr - Kq - \int (Ke^y - K)^+ \nu (dy) = Kd < 0 \end{aligned}$$
which is a contradiction. Hence \(x^* < K\) and \(\lim _{\varepsilon \rightarrow 0} \frac{c_0(x_\varepsilon , \varepsilon )}{\varepsilon }=0\). In particular, \(x^*\) solves
$$\begin{aligned} Kr = x^* q + \int (x^* e^y - K)^+ \nu (dy). \end{aligned}$$
\(\square \)
Conclusions
We offer a new perspective on the determination of the critical price of the American put option at maturity when the jump-adjusted dividend yield of the underlying stock is either greater than or weakly smaller than the riskfree rate. Our approach is rigorous without sacrificing financial intuition.
We carefully review the analysis proposed by Ingersoll (1998), who uses an indifference-point argument to intuitively assess why, under the Black and Scholes (1973) model, the critical price displays a discontinuity at maturity if the dividend yield (jumps are absent) is greater than the riskfree rate. His indifference-point argument is plagued by the exclusion of the early exercise premium.
By showing that the exclusion is acceptable and that the indifference-point argument can be extended to a jump-diffusive setting, we bring a fresh economical and technical contribution to the rich literature on the close-to-maturity behavior of the critical prices related to finite-maturity American options. While there have been several technical studies of such a behavior in the presence of the early exercise premium under various settings, we are the first to rigorously corroborate of the economic argument proposed by Ingersoll (1998), to extend it to a jump-diffusive setting, and to emphasize the computational equivalence at maturity of an American option problem to a simpler European option problem under the models we use.
Our findings are propitious for the analysis of the critical price of the American put option at maturity under richer models, as the possible exclusion of the early exercise premium greatly simplifies calculations.
Notes
-
When interest rates are negative a double free boundary may appear. Battauz et al 2012; 2015; 2020 show that in this case, under a diffusive dynamics, the upper free boundary is increasing, continuous and tends to the strike price at maturity, whereas the lower free boundary is decreasing, continuous everywhere but at maturity, where it exhibits a discontinuity. The double continuation region in the Lévy model has been investigated for the perpetual case by De Donno et al. (2020).
-
Lamberton (1995) shows a similar result for the diffusive case and no dividends.
-
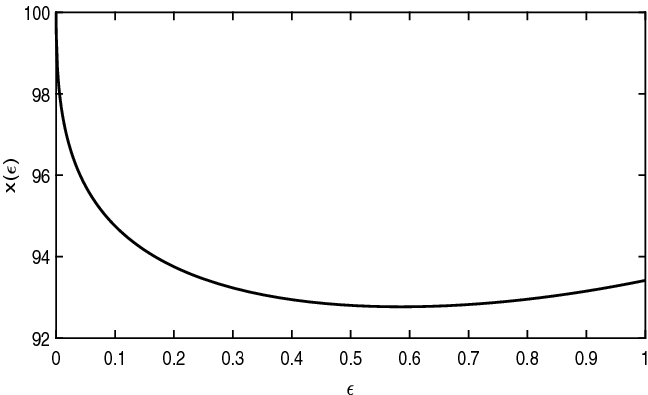
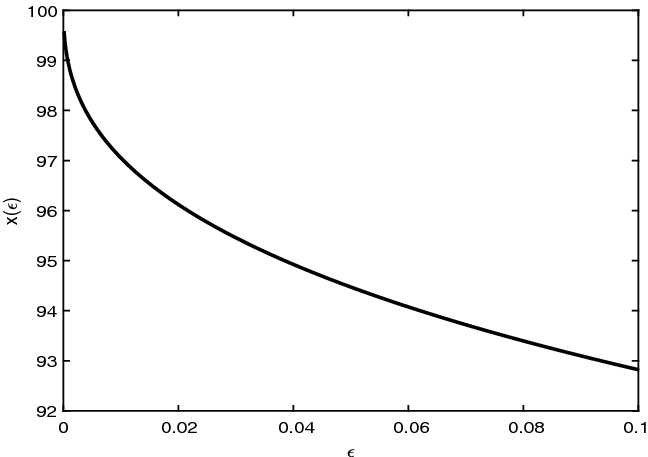
In Appendix B we show numerically that \(x(\varepsilon )\) is monotone in a neighborhood of 0, and thus \(x(\varepsilon )\) converges as \( \varepsilon \rightarrow 0.\)
-
In fact, Theorem 4.1 can be seen as a special case of Theorem 4.2.
-
For the case \(r=q\), a similar remark can be find in Lamberton and Villeneuve (2003)
-
To solve Eq. (3.3), we neglect the terms with more than 3 jumps in the infinite sum which defines the price of the European put option. These terms are \(o(\varepsilon ^{3})\) so their contribution is negligible when \(\varepsilon \) is close to 0.
References
-
Barles, G., Burdeau, J., Romano, M., & Sansoen, N. (1995). Critical stock price near expiration. Mathematical Finance, 5, 77–95.
-
Battauz, A., De Donno, M., & Sbuelz, A. (2012). Real options with a double continuation region. Quantitative Finance, 12(3), 465–475.
-
Battauz, A., De Donno, M., & Sbuelz, A. (2015). Real options and american derivatives: The double continuation region. Management Science, 61(5), 1094–1107.
-
Battauz, A., De Donno, M., & Sbuelz, A. (2020). On the exercise of American Quanto Options, Working paper.
-
Black, F., & Cox, J. C. (1976). Valuing corporate securities: Some effects of bond indenture provisions. The Journal of Finance, 31(2), 351–367.
-
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. The Journal of Political Economy, 81(3), 637–654.
-
Bouselmi, A., & Lamberton, D. (2016). The critical price of the american put near maturity in the jump-diffusion model. SIAM Journal of Financial Mathematics, 7, 236–272.
-
Cheng, J., & Zhang, J. E. (2012). Analytical pricing of American options. Review of Derivatives Research, 15, 157–192.
-
De Donno, M., Palmowski, Z., & Tumilewicz, J. (2020). Double continuation regions for American and swing options with negative discount rate in Lévy models. Mathematical Finance, 30(1), 196–227.
-
Detemple, J. (2005). American-style derivatives: Valuation and computation. London: Chapman and Hall.
-
El Karoui, N. (1981). Les aspects probabilistes du controle stochastique. In Ecole d'Etė de Probabilitės deSaint Flour, IX, 1979. Lecture Notes in Mathematics, 876, 74–238.
-
Evans, J. D., Kuske, R., & Keller, J. B. (2002). American options on asset with dividends near expiry. Mathematical Finance, 12, 219–237.
-
Gerer, J., & Dorfleitner, G. (2018). Optimal discrete hedging of American options using an integrated approach to options with complex embedded decisions. Review of Derivatives Research, 21, 175–199.
-
Geske, R. (1977). The valuation of corporate liabilities as compound option. Journal of Financial and Quantitative Analysis, 12(4), 541–552.
-
Henderson, V., & Hobson, D. (2008). Perpetual American options in incomplete markets: The infinitely divisible case. Quantitative Finance, 8, 461–469.
-
Henderson, V., Sun, J., & Whalley, A. E. (2014). Portfolios of American options under general preferences: Results and counterexamples. Mathematical Finance, 24, 533–566.
-
Huang, J.-Z., Subrahmanyam, M., & Yu, G. (1996). pricing and hedging American options: A recursive investigation method. Review of Financial Studies, 9(1), 277–300.
-
Ingersoll, J. E. (1998). Approximating American options and other financial contracts using barrier derivatives. Journal of Computational Finance, 2(1), 85–112.
-
Kim, I. J., & Yu, G. (1996). An alternative approach to the valuation of American options and applications. Review of Derivatives Research, 1, 61–85.
-
Lamberton, D. (1995). Critical price for an American option near maturity. In E. Bolthausen, M. Dozzi, & F. Russo (Eds.), Seminar on stochastic analysis. Boston: Birkhäuser.
-
Lamberton, D., & Mikou, M. (2008). The critical price of the American put in an exponential Lévy model. Finance and Stochastics, 12, 561–581.
-
Lamberton, D., & Villeneuve, S. (2003). Critical price near maturity for an American option on dividend-paying stock. Annals of Applied Probability, 13, 800–815.
-
Li, M. (2010a). Analytical approximations for the critical stock prices of American options: A performance comparison. Review of Derivatives Research, 13, 75–99.
-
Li, M. (2010b). A quasi-analytical interpolation method for pricing American options under general multi-dimensional diffusion. Review of Derivatives Research, 13, 177–217.
-
Pham, H. (1997). Optimal stopping, free boundary, and American option in a jump-diffusion model. Applied Mathematics and Optimization, 35, 145–164.
-
Vidal Nunes, J. P. (2011). American options and callable bonds under stochastic interest rates and endogenous bankruptcy. Review of Derivatives Research, 14, 283–332.
Funding
Open access funding provided by Università Commerciale Luigi Bocconi within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Marzia De Donno: This research has financially been supported by the Programme "FIL-Quota Incentivante" of University of Parma and co-sponsored by Fondazione Cariparma.
Appendices
A Proofs
Proof of Lemma 4.1
From Lemma 3.1, we know that \(x(\varepsilon )\) is the solution to the equation Footnote 5 \(F(x(\varepsilon ), \varepsilon ) = 0\) where
$$\begin{aligned} F\left( x,\varepsilon \right) = p(x, \varepsilon ) - (K - x) \end{aligned}$$
(A.1)
The implicit function theorem implies that \(x(\varepsilon )\) is differentiable on (0,T) and
$$\begin{aligned} x^{\prime }(\varepsilon )=-\frac{F_{\varepsilon }}{F_{x}}= - \frac{ p_\varepsilon (x(\varepsilon ), \varepsilon )}{1+p_x(x(\varepsilon ), \varepsilon )} \end{aligned}$$
(A.2)
We first show that, independently by the value of the limit of \( x(\varepsilon )\),
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}c(x(\varepsilon ),\varepsilon )=0. \end{aligned}$$
(A.3)
To this aim, we recall that the call option price is given by the Black-Scholes formula
$$\begin{aligned} c(x,\varepsilon )=xe^{-q\varepsilon }N\left( d_{1}\right) -Ke^{-r\varepsilon }N\left( d_{2}\right) \end{aligned}$$
(A.4)
where N(z) denotes in this Proof the distribution function of a standard normal random variable, while
$$\begin{aligned} d_{1}=\frac{1}{\sigma \sqrt{\varepsilon }}\left( \ln \left( \dfrac{x}{K} \right) +\left( r-q+\dfrac{1}{2}\sigma ^{2}\right) \varepsilon \right) \text { and }d_{2}=d_{1}-\sigma \sqrt{\varepsilon }. \end{aligned}$$
(A.5)
Now, if \(\lim _{\varepsilon \rightarrow 0}x(\varepsilon )=K\) then \( d_{1},d_{2}\rightarrow 0,\) hence \(N\left( d_{1}\right) ,N\left( d_{2}\right) \rightarrow \frac{1}{2},\) and \(c(x(\varepsilon ),\varepsilon )=x(\varepsilon )e^{-q\varepsilon }N\left( d_{1}\right) -Ke^{-r\varepsilon }N\left( d_{2}\right) \rightarrow 0\) yielding (A.3). On the other hand, if \(\lim _{\varepsilon \rightarrow 0}x(\varepsilon )=x^{*}<K\) then \( d_{1},d_{2}\rightarrow -\infty ,\) hence \(N\left( d_{1}\right) ,N\left( d_{2}\right) \rightarrow 0.\) and as a consequence we still have (A.3). This implies that we can apply L'Hopital's rule to find
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{ \varepsilon }=\lim _{\varepsilon \rightarrow 0}\frac{\frac{d}{d\varepsilon } c(x(\varepsilon ),\varepsilon )}{1} \end{aligned}$$
By the chain rule, we have that \(\frac{d}{d\varepsilon }c(x(\varepsilon ), \varepsilon ) =c_{x}x^{\prime }(\varepsilon )+c_{\varepsilon }\). The derivatives of the call option price are (from Equation (A.4) )
$$\begin{aligned} c_{x}=e^{-q\varepsilon }N\left( d_{1}\right) \end{aligned}$$
since
$$\begin{aligned} xe^{-q\varepsilon }N^{\prime }\left( d_{1}\right)&=Ke^{-r\varepsilon }N^{\prime }\left( d_{2}\right) \nonumber \\ \frac{\partial d_{1}}{\partial x}&=\frac{\partial d_{2}}{\partial x}, \end{aligned}$$
(A.6)
and
$$\begin{aligned} c_{\varepsilon } =-qxe^{-q\varepsilon }N\left( d_{1}\right) +rKe^{-r\varepsilon }N\left( d_{2}\right) +xe^{-q\varepsilon }N^{\prime }\left( d_{1}\right) \frac{\partial d_{1}}{\partial \varepsilon }-Ke^{-r \varepsilon }N^{\prime }\left( d_{2}\right) \frac{\partial d_{2}}{\partial \varepsilon }. \end{aligned}$$
Since \(\frac{\partial d_{1}}{\partial \varepsilon }=\frac{\partial d_{2}}{ \partial \varepsilon }+\sigma \frac{1}{2\sqrt{\varepsilon }}\), we obtain
$$\begin{aligned} c_{\varepsilon }=-qxe^{-q\varepsilon }N\left( d_{1}\right) +rKe^{-r\varepsilon }N\left( d_{2}\right) +Ke^{-r\varepsilon }N^{\prime }\left( d_{2}\right) \sigma \frac{1}{2\sqrt{\varepsilon }}. \end{aligned}$$
Exploiting the put-call parity in the computations of \(p_\varepsilon \) and \( p_x\), we can rewrite \(x^{\prime }(\varepsilon )\) as
$$\begin{aligned} x^{\prime }(\varepsilon )= \frac{rKe^{-r\ \varepsilon }-x(\varepsilon )qe^{-q\varepsilon }-c_{\varepsilon }(x(\varepsilon ),\varepsilon )}{1-e^{-q\varepsilon }+c_{x}(x(\varepsilon ),\varepsilon )} \end{aligned}$$
(A.7)
So, we have that (for sake of simplicity, we omit the dependence of x on \( \varepsilon \) and of \(c_x\) and \(c_\varepsilon \) on x and \(\varepsilon \))
$$\begin{aligned}&\frac{d}{d\varepsilon }c(x(\varepsilon ),\varepsilon ) =c_{x}\underset{ x^{\prime }(\varepsilon )}{\underbrace{\frac{rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon }-c_{\varepsilon }}{1-e^{-q\varepsilon }+c_{x}}}} +c_{\varepsilon } \\&=\frac{c_{x}rKe^{-r\ \varepsilon }-c_{x}xqe^{-q\varepsilon }+c_{\varepsilon }(1-e^{-q\varepsilon }) }{ (1-e^{-q\varepsilon }) +c_{x}} \\&=\frac{\left( rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon }\right) \left( 1-e^{-q\varepsilon } +c_{x}\right) -(1-e^{-q\varepsilon }) \left( rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon }\right) +c_{\varepsilon }(1-e^{-q\varepsilon }) }{1-e^{-q\varepsilon }+c_{x}} \\&=rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon }-\frac{(1-e^{-q\varepsilon }) \left( rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon }+c_{\varepsilon }\right) }{ 1-e^{-q\varepsilon }+c_{x}}. \end{aligned}$$
If \(\lim _{\varepsilon \rightarrow 0}x(\varepsilon )=x^{*}=K,\) then \(c_{x}=e^{-q\varepsilon }N\left( d_{1}\right) \rightarrow \frac{1}{2},\) and
$$\begin{aligned} \varepsilon c_{\varepsilon }&=\varepsilon \left( -qxe^{-q\varepsilon }N\left( d_{1}\right) +rKe^{-r\varepsilon }N\left( d_{2}\right) +Ke^{-r\varepsilon }N^{\prime }\left( d_{2}\right) \sigma \frac{1}{2\sqrt{ \varepsilon }}\right) \sim KN^{\prime }\left( d_{2}\right) \sigma \frac{\sqrt{ \varepsilon }}{2} \end{aligned}$$
leading to \(\frac{(1-e^{-q\varepsilon }) \left( rKe^{-r\ \varepsilon }-x(\varepsilon )qe^{-q\varepsilon }+c_{\varepsilon }\right) }{ 1-e^{-q\varepsilon }+c_{x}}\sim \frac{KN^{\prime }\left( d_{2}\right) \sigma \frac{\sqrt{\varepsilon }}{2}}{0.5}\) and therefore
$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{ \varepsilon } \\&=\lim _{\varepsilon \rightarrow 0} \left( rKe^{-r\ \varepsilon }-x(\varepsilon ) qe^{-q\varepsilon }-\frac{(1-e^{-q\varepsilon }) \left( rKe^{-r\ \varepsilon }-x(\varepsilon )qe^{-q\varepsilon }+c_{\varepsilon }\right) }{ 1-e^{-q\varepsilon }+c_{x}} \right) \\&=rK-Kq \end{aligned}$$
so case (i) is proved.
Assume now that \(\lim _{\varepsilon \rightarrow 0}x(\varepsilon )=x^{*}<K.\) In this case \(c_{x}=e^{-q\varepsilon }N\left( d_{1}\right) \rightarrow 0, \) and
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\frac{c_{x}}{\varepsilon }&=\lim _{\varepsilon \rightarrow 0}\frac{e^{-q\varepsilon }N\left( d_{1}\right) }{ \varepsilon }=\lim _{\varepsilon \rightarrow 0}\frac{N\left( d_{1}\right) }{ \varepsilon } \\&=\lim _{\varepsilon \rightarrow 0}\frac{\frac{d}{d\varepsilon }N\left( d_{1}\right) }{1}=\lim _{\varepsilon \rightarrow 0}N^{\prime }\left( d_{1}\right) \left( \frac{\partial d_{1}}{\partial x}x^{\prime }(\varepsilon )+ \frac{\partial d_{1}}{\partial \varepsilon }\right) \end{aligned}$$
Now
$$\begin{aligned} N^{\prime }\left( d_{1}\right) \frac{\partial d_{1}}{\partial \varepsilon } =N^{\prime }\left( d_{1}\right) \frac{\partial \left( \frac{1}{\sigma \sqrt{ \varepsilon }}\ln \left( \dfrac{x}{K}\right) +\left( r-q+\dfrac{1}{2} \sigma ^{2}\right) \frac{\sqrt{\varepsilon }}{\sigma }\right) }{\partial \varepsilon }\sim \frac{\frac{1}{2\sqrt{\pi }}e^{-\frac{d_{1}^{2}}{2}}}{\sqrt{ \varepsilon ^{3}}}\rightarrow 0. \end{aligned}$$
To evaluate \(\lim _{\varepsilon \rightarrow 0} N^{\prime }(d_1) \frac{ \partial d_{1}}{\partial x}x^{\prime }(\varepsilon )\) we observe that
$$\begin{aligned} \displaystyle \frac{\partial d_{1}}{\partial x} =\frac{1}{x\sigma \sqrt{ \varepsilon }}. \end{aligned}$$
Moreover, since \(d_{2}^{{}}\sim \frac{1}{\sigma \sqrt{\varepsilon }}\left( \ln \left( \dfrac{x^{*}}{K}\right) \right) \), we have that
$$\begin{aligned} \frac{N^{\prime }\left( d_{2}\right) }{\sqrt{\varepsilon }}=\frac{1}{2\sqrt{\pi }}e^{-\frac{d_{2}^{2}}{2}}\frac{1}{\sqrt{\varepsilon }}\rightarrow 0 \end{aligned}$$
which implies
$$\begin{aligned} c_{\varepsilon }=-qxe^{-q\varepsilon }N\left( d_{1}\right) +rKe^{-r\varepsilon }N\left( d_{2}\right) +Ke^{-r\varepsilon }N^{\prime }\left( d_{2}\right) \sigma \frac{1}{2\sqrt{\varepsilon }}\sim Ke^{-r\varepsilon }N^{\prime }\left( d_{2}\right) \sigma \frac{1}{2\sqrt{ \varepsilon }}\rightarrow 0, \end{aligned}$$
hence
$$\begin{aligned} x^{\prime }(\varepsilon )=\frac{rKe^{-r\ \varepsilon }-xqe^{-q\varepsilon } -c_{\varepsilon }}{1-e^{-q\varepsilon }+c_{x}}\sim \frac{rK-xq}{ q\varepsilon +c_{x}}. \end{aligned}$$
So
$$\begin{aligned} N^{\prime }\left( d_{1}\right) \frac{\partial d_{1}}{\partial x} x^{\prime }(\varepsilon )&\sim \frac{1}{2\sqrt{\pi }}e^{-\frac{d_{1}^{2}}{2}} \frac{1}{x\sigma \sqrt{\varepsilon }}\frac{rK-xq}{q\varepsilon +c_{x}} \sim e^{-\frac{d_{1}^{2}}{2}}\frac{1}{x\sigma \sqrt{\varepsilon }}\frac{rK-xq}{ q\varepsilon +c_{x}} \end{aligned}$$
Lastly, \(d_{1}\rightarrow -\infty \) yields
$$\begin{aligned} c_{x}e^{\frac{d_{1}^{2}}{2}}=\frac{c_{x}}{e^{-\frac{d_{1}^{2}}{2}}}\sim \frac{N\left( d_{1}\right) }{e^{-\frac{d_{1}^{2}}{2}}}\sim \frac{N^{\prime }\left( d_{1}\right) }{-d_{1}e^{-\frac{d_{1}^{2}}{2}}}\sim \frac{e^{-\frac{ d_{1}^{2}}{2}}}{-d_{1}e^{-\frac{d_{1}^{2}}{2}}}\rightarrow 0 \end{aligned}$$
and \(\varepsilon \sqrt{\varepsilon }e^{\frac{d_{1}^{2}}{2}}\rightarrow +\infty .\) Therefore, we can conclude that
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}N^{\prime }(d_1) \frac{\partial d_{1}}{ \partial x}x^{\prime }(\varepsilon )&=\lim _{\varepsilon \rightarrow 0}\frac{1 }{2\sqrt{\pi }x \sigma }\frac{rK-xq}{q\varepsilon \sqrt{\varepsilon }e^{\frac{ d_{1}^{2}}{2}}+\sqrt{\varepsilon }c_{x}e^{\frac{d_{1}^{2}}{2}}} =0 \end{aligned}$$
and \(\lim _{\varepsilon \rightarrow 0}\frac{c_x }{\varepsilon } = 0\). As a consequence, \(\lim _{\varepsilon \rightarrow 0}\frac{c(x(\varepsilon ),\varepsilon )}{\varepsilon } = \lim _{\varepsilon \rightarrow 0} c_x x^{\prime }(\varepsilon )+ c_\varepsilon = 0.\) \(\square \)
Proof of Lemma 4.2
We can proceed as in the diffusive case and exploit the implicit function theorem to obtain the regularity properties of \(x(\varepsilon )\) and to compute its derivative. To prove (i), we observe that:
$$\begin{aligned} c_n(x(\varepsilon ), \varepsilon )= & {} \mathbb {\ E}_{T- \varepsilon } \left[ e^{-r \varepsilon } (S_T-K)^+ | S_{T- \varepsilon } = x(\varepsilon ), N_T - N_{T- \varepsilon } = n\right] \\\le & {} \mathbb {\ E}_{T- \varepsilon } \left[ e^{-r \varepsilon } S_T | S_{T- \varepsilon } = x(\varepsilon ), N_T - N_{T- \varepsilon } = n\right] \\= & {} x(\varepsilon ) \mathbb {\ E}\left[ e^{\left( -q-m\lambda - \frac{\sigma ^2}{ 2}\right) \varepsilon + \sigma (W_T-W_{T- \varepsilon })+\sum _{j=1}^n U_j} \right] \\= & {} x(\varepsilon ) e^{\left( -q-m\lambda \right) \varepsilon }(1+m)^n \le K (1+m)^n \end{aligned}$$
Hence
$$\begin{aligned} 0\le & {} \frac{1}{\varepsilon } \sum _{n \ge 2 } e^{-\lambda \varepsilon } \frac{{(\lambda \varepsilon )}^n}{n!} c_n(x(\varepsilon ), \varepsilon ) \\\le & {} \sum _{n=2}^{+\infty } e^{-\lambda \varepsilon } \frac{{\lambda }^n {( \varepsilon )}^{n-1}}{n!} c_n(x(\varepsilon ), \varepsilon ) \\\le & {} K\, \sum _{n=2}^{+\infty } e^{-\lambda \varepsilon } \frac{{\lambda }^n {( \varepsilon )}^{n-1}}{n!} (1+m)^n \\= & {} K\,\varepsilon e^{-\lambda \varepsilon } \lambda ^2 (1+m)^2 \sum _{n=2}^{+\infty } \frac{(\lambda (1+m) ( \varepsilon ))^{n-2}}{n (n-1) (n-2) !} \\= & {} K\, \varepsilon e^{-\lambda \varepsilon } \lambda ^2 (1+m)^2 \sum _{k=0}^{+\infty } \frac{(\lambda (1+m) ( \varepsilon ))^{k}}{(k+2) (k+1) k! } \\\le & {} K\, \varepsilon e^{-\lambda \varepsilon } \lambda ^2 (1+m)^2 \sum _{k=0}^{+\infty } \frac{(\lambda (1+m) ( \varepsilon ))^{k}}{k!} \\= & {} K\, \varepsilon e^{-\lambda \varepsilon } \lambda ^2 (1+m)^2 e^{\lambda (1+m) \varepsilon } \rightarrow 0 \qquad {\text{ a }s } \ \varepsilon \rightarrow 0. \end{aligned}$$
We now prove (ii), namely that \(\lim _{ \varepsilon \rightarrow 0} c_1 (x(\varepsilon ), \varepsilon ) = E\left( (x^*e^{U_1} - K)^+\right] \). Denote \( Y_{\varepsilon } = (r-q-\frac{\sigma ^2}{2} - m\lambda )\varepsilon + \sigma W(\varepsilon )\). Then
$$\begin{aligned} c_1 (x(\varepsilon ), \varepsilon )= & {} e^{-r\varepsilon } E\left[ (x(\varepsilon ) e^{Y_{\varepsilon } +{U_1}} - K)^+\right] \\= & {} e^{-r\varepsilon } \left( E\left[ (K-x(\varepsilon ) e^{Y_{\varepsilon } +{U_1 }})^+\right] + E\left[ x(\varepsilon )^{Y_{\varepsilon } +{U_1}}\right] - K\right) \end{aligned}$$
The family \(Y_{\varepsilon }\) is distributed as \({\mathcal {N}} \left( (r-q-\frac{ \sigma ^2}{2}-m\lambda )\varepsilon , \sigma ^2 \varepsilon \right) \) hence it converges in distribution to the constant 0 as \(\varepsilon \rightarrow 0\). Being \( U_1\) independent of \(Y_\varepsilon \), the sum \((Y_\varepsilon + U_1)\) converges in distribution to \(U_1\) and the sum \((\ln x(\varepsilon ) + Y_\varepsilon + U_1)\) converges in distribution to \(\ln x^* + U_1\). Since \( f(z) = (K-e^z)^+\) is continuous and bounded, we have (Theorem 18.1 in Jacod-Protter) that
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} E\left[ (K- e^{\ln x(\varepsilon )+ Y_{\varepsilon } +{ U_1}})^+\right] = E\left[ (K- e^{\ln x^* + {U_1}})^+\right] =E\left[ (K-x^* e^{ {U_1}})^+\right] . \end{aligned}$$
We exploit again the independence between \(Y_{\varepsilon }\) and \({U_1}\) to show that
$$\begin{aligned} E\left[ x(\varepsilon ) e^{Y_{\varepsilon } +{U_1}}\right]= & {} x(\varepsilon ) E \left[ e^{{U_1}}\right] E\left[ e^{Y_{\varepsilon }}\right] \\= & {} x(\varepsilon ) E \left[ e^{{U_1}}\right] e^{(r-q-m\lambda )\varepsilon } \rightarrow x^* E\left[ e^{{U_1} }\right] \quad \text{ as } \varepsilon \rightarrow 0. \end{aligned}$$
Therefore
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} c_1(x(\varepsilon ), \varepsilon )= & {} E\left[ (K-x^*e^{{ U_1}})^+\right] + E\left[ x^*e^{{U_1}}\right] - K \\= & {} E\left[ (x^*e^{U_1} - K)^+ \right] =\int (x^* e^y - K)^+ \mu (dy). \end{aligned}$$
Finally, we have to prove (iii). The function \(c_0\) denotes the price of an out of the money call option when no jumps occur till maturity, namely in the diffusive case. We can then show, as in Lemma 4.1, that \(\lim _{\varepsilon \rightarrow 0} c_0(x(\varepsilon ), \varepsilon ) = 0\) and employ L'Hospital's rule to compute
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \frac{c_0(x(\varepsilon ), \varepsilon )}{\varepsilon } = \lim _{\varepsilon \rightarrow 0}\frac{\frac{d}{d\varepsilon } c(x(\varepsilon ),\varepsilon )}{1} = \lim _{\varepsilon \rightarrow 0} \frac{\partial c_{0}(x(\varepsilon ), \varepsilon )}{\partial x} \cdot x^{\prime }(\varepsilon )+\frac{\partial c_{0}(x(\varepsilon ), \varepsilon )}{ \partial \varepsilon } \end{aligned}$$
where, as in the previous case, Dini's theorem yields
$$\begin{aligned} x^{\prime }(\varepsilon )= \frac{rKe^{-r\ \varepsilon }-x(\varepsilon )qe^{-q\varepsilon }-c_{\varepsilon }(x(\varepsilon ),\varepsilon )}{1-e^{-q\varepsilon }+c_{x}(x(\varepsilon ),\varepsilon )} \end{aligned}$$
For sake of simplicity, let \(c_{n,x} = \frac{\partial c_n}{\partial x}\) and \( c_{n,\varepsilon } = \frac{\partial c_n}{\partial \varepsilon }\) Then
$$\begin{aligned} c_x = e^{-\lambda \varepsilon } c_{0,x} + \sum _{n \ge 1} e^{-\lambda \varepsilon } \frac{(\lambda \varepsilon )^n}{n!}c_{n,x}. \end{aligned}$$
Note that, since the delta of a call option is always positive and smaller than 1, we have
$$\begin{aligned} 0 \le \sum _{n \ge 1} e^{-\lambda \varepsilon } \frac{(\lambda \varepsilon )^n}{ n!}c_{n,x} \le \sum _{n \ge 1} e^{-\lambda \varepsilon } \frac{ (\lambda \varepsilon )^n}{n!} = 1 - e^{-\lambda \varepsilon } \end{aligned}$$
hence it goes to 0 as \(\varepsilon \) tends to 0. As a consequence, \(c_x \sim c_{0, x}\) as \(\varepsilon \rightarrow 0\). Similarly
$$\begin{aligned} c_\varepsilon =-\lambda e^{-\lambda \varepsilon } c_{0} + e^{-\lambda \varepsilon } c_{0,\varepsilon } -\lambda ^2 \varepsilon e^{-\lambda \varepsilon } c_{1} + \lambda e^{-\lambda \varepsilon } c_{1} + \lambda \varepsilon e^{-\lambda \varepsilon } c_{1,\varepsilon } + \frac{\partial }{ \partial \varepsilon } \left( \sum _{n \ge 2} e^{-\lambda \varepsilon } \frac{ (\lambda \varepsilon )^n}{n!}c_{n}\right) . \end{aligned}$$
The last term in the above equality goes to 0, since we can show, as in (i), that
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \frac{\partial }{\partial \varepsilon } \left( \sum _{n \ge 2} e^{-\lambda \varepsilon } \frac{(\lambda \varepsilon )^n}{n!} c_{n}\right) = \lim _{\varepsilon \rightarrow 0} \frac{1}{\varepsilon } \left( \sum _{n \ge 2} e^{-\lambda \varepsilon } \frac{(\lambda \varepsilon )^n}{n!} c_{n}\right) =0. \end{aligned}$$
Hence \(c_\varepsilon \sim c_{0, \varepsilon } + \lambda c_1 \) as \(\varepsilon \rightarrow 0\) (recall that \(c_0\) is the price of a European call option when no jumps occur, that is in the standard Black and Scholes market, so it behaves like c in Lemma 4.1. So we have
$$\begin{aligned} x^{\prime }(\varepsilon ) \sim \frac{rK-x(\varepsilon )q - c_{0, \varepsilon } - \lambda c_1}{1-e^{-q\varepsilon }+c_{0, x}} \end{aligned}$$
and rearranging the terms,
$$\begin{aligned} c_{0,x} x^{\prime }(\varepsilon ) + c_{0, \varepsilon } \sim rK-x(\varepsilon )q- \lambda c_1 - \frac{( rK-x(\varepsilon )q- \lambda c_1-c_{0, \varepsilon })(1-e^{-q\varepsilon })}{1-e^{-q\varepsilon }+c_{0, x}} \end{aligned}$$
Exploiting the same arguments as in the proof of Lemma 4.1 and recalling (ii), we prove the claim. \(\square \)
B Numerical convergence of the European critical price
The aim of this section is to show numerically that \(x(\varepsilon )\) converges to some \(x^{*}\in (0,K]\) when \(\varepsilon \) tends to 0.
To find \(x(\varepsilon )\), we solve numerically Eq. (3.3) for small values of \(\varepsilon \), approaching 0. For the jump-diffusion model, we consider the case of either constant or gaussian (either positive ore negative) jumps. Footnote 6
When jumps are assumed to be constant, \(U_j =\ln (1+m)\), with \(m\in {\mathbb {R}}\): in this case, \(d=r-q\) when jumps are negative (\(m<0\)) and \( d=r-q-m\lambda \) when jumps are positive (\(m>0\)). In the case of Gaussian jumps, we assume \(U_j\) to have a normal distribution with expectation a and variance \(b^2\) (\(a\in {\mathbb {R}}, b > 0\)), hence \(d=r-q - \lambda e^{a + b^2/2} N\left( \frac{a+b^2}{b} \right) + \lambda N\left( \frac{a}{b} \right) \), where N denotes here the distribution function of a standard normal random variable.
We fix \(K = 100\), \(\sigma = 0.2\) for the diffusive model and \(\sigma = 0.15\) for the jump-diffusion model. We then let the other parameters vary in order to analyze the two cases, \(d\ge 0\) and \(d < 0\). The results in the various models are very similar and are depicted in the figures below.
We observe that \(x(\varepsilon )\) is always monotone in a neighborhood of 0, thus validating our claim. When \(d\ge 0\) (\(r\ge q\) in the diffusive model) \( x(\varepsilon )\) approaches the critical price, which coincides with the strike price, from below, namely \(x(\varepsilon )\) is decreasing with respect to time to maturity (see Figures 2, 3 and 4 ).
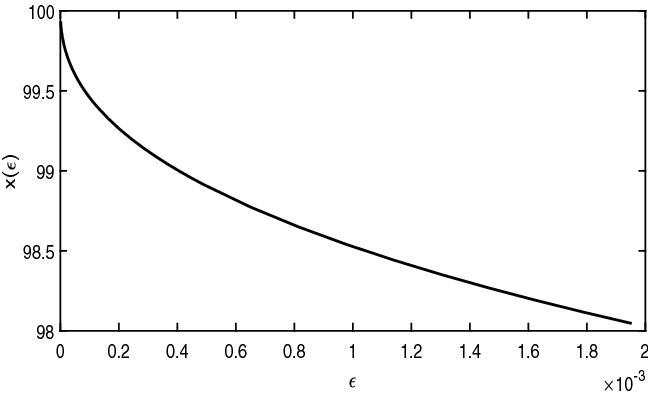
Geometric brownian motion (\(r\ge q\)) \(r=0.03\), \(q=0.01\)
Jump diffusion, constant jumps (\(d\ge 0\)) \(r = 0.04, q = 0.01, \lambda = 1, m = 0.02\)
Jump diffusion, gaussian jumps (\(d\ge 0\)) \(r = 0.03, q = 0.01, \lambda =1,a = -0.1, b=0.1 \)
When \(d<0\), \( x(\varepsilon )\) approaches monotonically a finite value, which is strictly smaller than the strike price (see Figures 5, 6 and 7).
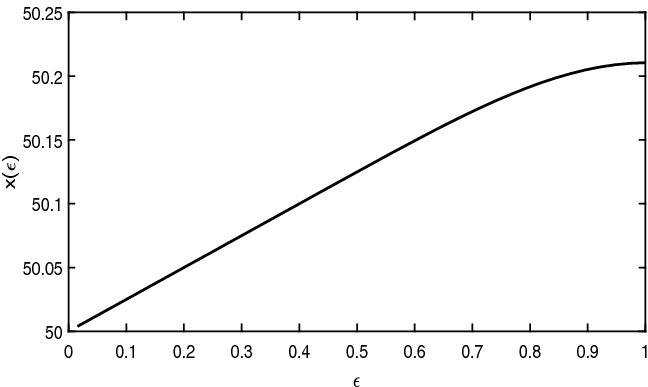
Geometric brownian motion (\(r<q\)) \(r=0.01, q=0.02\)
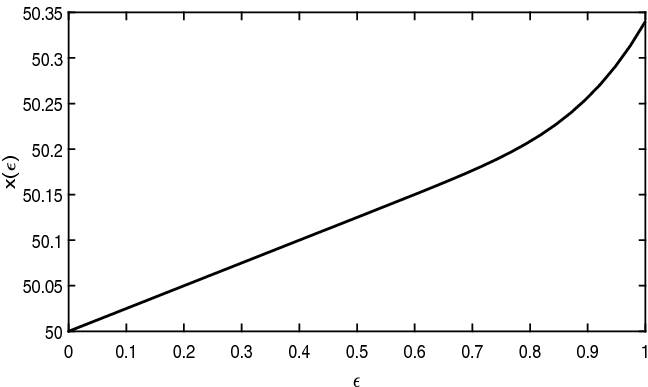
Jump diffusion, constant jumps (\(d<0\)) \(r = 0.01, q = 0.02, \lambda = 2, m = 0.1 \)
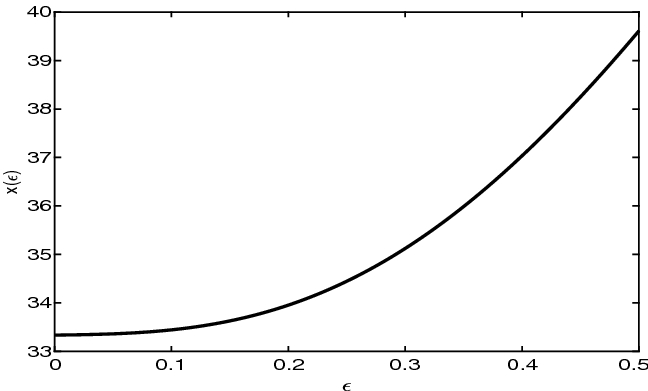
Jump diffusion, normal jumps (\(d<0\)) \(r = 0.01, q = 0.03, \lambda = 1, a = 0.05, b=0.1 \)
Such limits have been analytically computed in Theorems 4.1 and 4.2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Battauz, A., De Donno, M., Gajda, J. et al. Optimal exercise of American put options near maturity: A new economic perspective. Rev Deriv Res 25, 23–46 (2022). https://doi.org/10.1007/s11147-021-09180-w
-
Accepted:
-
Published:
-
Issue Date:
-
DOI : https://doi.org/10.1007/s11147-021-09180-w
Keywords
- American options
- Valuation
- Optimal exercise
- Critical price
- European options
JEL Classification
- C02
- G12
woodplarriving1938.blogspot.com
Source: https://link.springer.com/article/10.1007/s11147-021-09180-w
0 Response to "The Continuation Value of the American to the Price of the European"
Post a Comment